AI & Machine Learning

Web3 Development

NFT & Metaverse

Blockchain Development

Blockchain Solutions

Products

Get in Touch
arrow-left Back to ‘Today at Nextrope Blog’

Monte Carlo Simulations in Tokenomics

Kajetan Olas

01 May 2024
Monte Carlo Simulations in Tokenomics

As the web3 field grows in complexity, traditional analytical tools often fall short in capturing the dynamics of digital markets. This is where Monte Carlo simulations come into play, offering a mathematical technique to model systems fraught with uncertainty.

Monte Carlo simulations employ random sampling to understand probable outcomes in processes that are too complex for straightforward analytic solutions. By simulating thousands, or even millions, of scenarios, Monte Carlo methods can provide insights into the likelihood of different outcomes, helping stakeholders make informed decisions under conditions of uncertainty.

In this article, we will explore the role of Monte Carlo simulations within the context of tokenomics.  illustrating how they are employed to forecast market dynamics, assess risk, and optimize strategies in the volatile realm of cryptocurrencies. By integrating this powerful tool, businesses and investors can enhance their analytical capabilities, paving the way for more resilient and adaptable economic models in the digital age.

Table of Contents

Understanding Monte Carlo Simulations

The Monte Carlo method is an approach to solving problems that involve random sampling to understand probable outcomes. This technique was first developed in the 1940s by scientists working on the atomic bomb during the Manhattan Project. The method was designed to simplify the complex simulations of neutron diffusion, but it has since evolved to address a broad spectrum of problems across various fields including finance, engineering, and research.

Random Sampling and Statistical Experimentation

At the heart of Monte Carlo simulations is the concept of random sampling from a probability distribution to compute results. This method does not seek a singular precise answer but rather a probability distribution of possible outcomes. By performing a large number of trials with random variables, these simulations mimic the real-life fluctuations and uncertainties inherent in complex systems.

Role of Randomness and Probability Distributions in Simulations

Monte Carlo simulations leverage the power of probability distributions to model potential scenarios in processes where exact outcomes cannot be determined due to uncertainty. Each simulation iteration uses randomly generated values that follow a specific statistical distribution to model different outcomes. This method allows analysts to quantify and visualize the probability of different scenarios occurring.

The strength of Monte Carlo simulations lies in the insight they offer into potential risks. They allow modelers to see into the probabilistic "what-if" scenarios that more closely mimic real-world conditions.

Monte Carlo Simulations in Tokenomics

Monte Carlo simulations are instrumental tool for token engineers. They're so useful due to their ability to model emergent behaviors. Here are some key areas where these simulations are applied:

Pricing and Valuation of Tokens

Determining the value of a new token can be challenging due to the volatile nature of cryptocurrency markets. Monte Carlo simulations help by modeling various market scenarios and price fluctuations over time, allowing analysts to estimate a token's potential future value under different conditions.

Assessing Market Dynamics and Investor Behavior

Cryptocurrency markets are influenced by a myriad of factors including regulatory changes, technological advancements, and shifts in investor sentiment. Monte Carlo methods allow researchers to simulate these variables in an integrated environment to see how they might impact token economics, from overall market cap fluctuations to liquidity concerns.

Assesing Possible Risks

By running a large number of simulations it’s possible to stress-test the project in multiple scenarios and identify emergent risks. This is perhaps the most important function of Monte Carlo Process, since these risks can’t be assessed any other way.

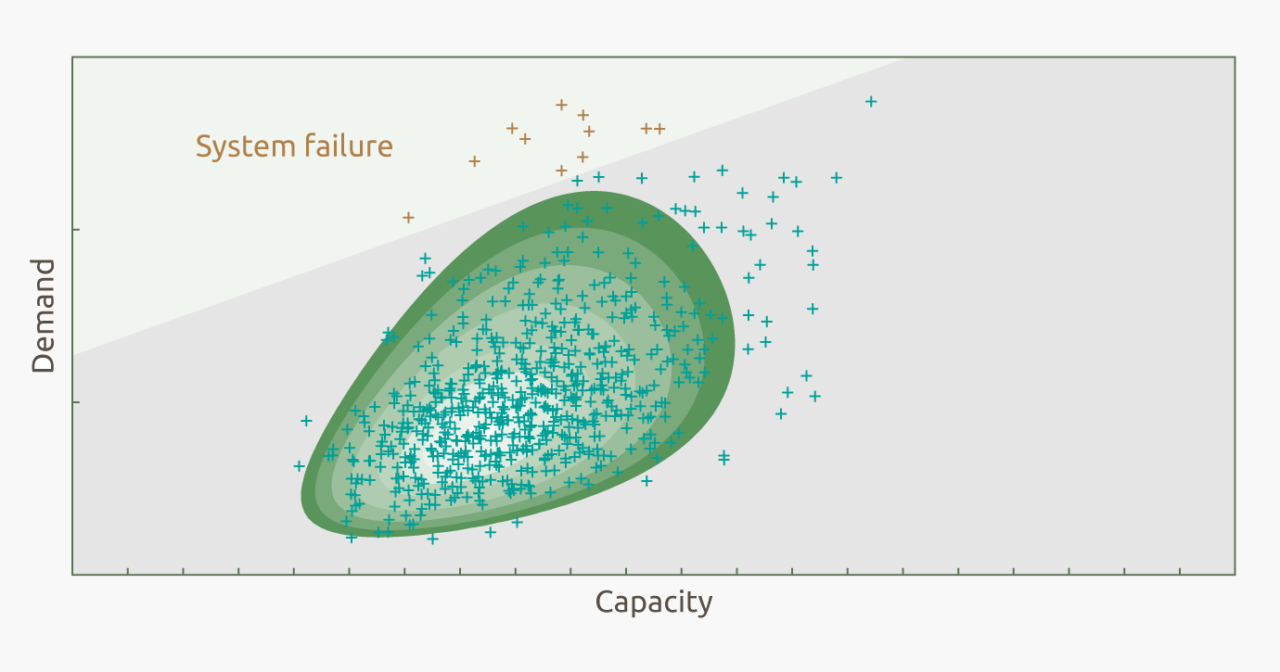
Source: How to use Monte Carlo simulation for reliability analysis?

Benefits of Using Monte Carlo Simulations

By generating a range of possible outcomes and their probabilities, Monte Carlo simulations help decision-makers in the cryptocurrency space anticipate potential futures and make informed strategic choices. This capability is invaluable for planning token launches, managing supply mechanisms, and designing marketing strategies to optimize market penetration.

Using Monte Carlo simulations, stakeholders in the tokenomics field can not only understand and mitigate risks but also explore the potential impact of different strategic decisions. This predictive power supports more robust economic models and can lead to more stable and successful token launches. 

Implementing Monte Carlo Simulations

Several tools and software packages can facilitate the implementation of Monte Carlo simulations in tokenomics. One of the most notable is cadCAD, a Python library that provides a flexible and powerful environment for simulating complex systems. 

Overview of cadCAD configuration Components

To better understand how Monte Carlo simulations work in practice, let’s take a look at the cadCAD code snippet:

sim_config = {

    'T': range(200),  # number of timesteps

    'N': 3,           # number of Monte Carlo runs

    'M': params       # model parameters

}

Explanation of Simulation Configuration Components

T: Number of Time Steps

  • Definition: The 'T' parameter in CadCAD configurations specifies the number of time steps the simulation should execute. Each time step represents one iteration of the model, during which the system is updated. That update is based on various rules defined by token engineers in other parts of the code. For example: we might assume that one iteration = one day, and define data-based functions that predict token demand on that day.

N: Number of Monte Carlo Runs

  • Definition: The 'N' parameter sets the number of Monte Carlo runs. Each run represents a complete execution of the simulation from start to finish, using potentially different random seeds for each run. This is essential for capturing variability and understanding the distribution of possible outcomes. For example, we can acknowledge that token’s price will be correlated with the broad cryptocurrency market, which acts somewhat unpredictably.

M: Model Parameters

  • Definition: The 'M' key contains the model parameters, which are variables that influence system's behavior but do not change dynamically with each time step. These parameters can be constants or distributions that are used within the policy and update functions to model the external and internal factors affecting the system.

Importance of These Components

Together, these components define the skeleton of your Monte Carlo simulation in CadCAD. The combination of multiple time steps and Monte Carlo runs allows for a comprehensive exploration of the stochastic nature of the modeled system. By varying the number of timesteps (T) and runs (N), you can adjust the depth and breadth of the exploration, respectively. The parameters (M) provide the necessary context and ensure that each simulation is realistic.

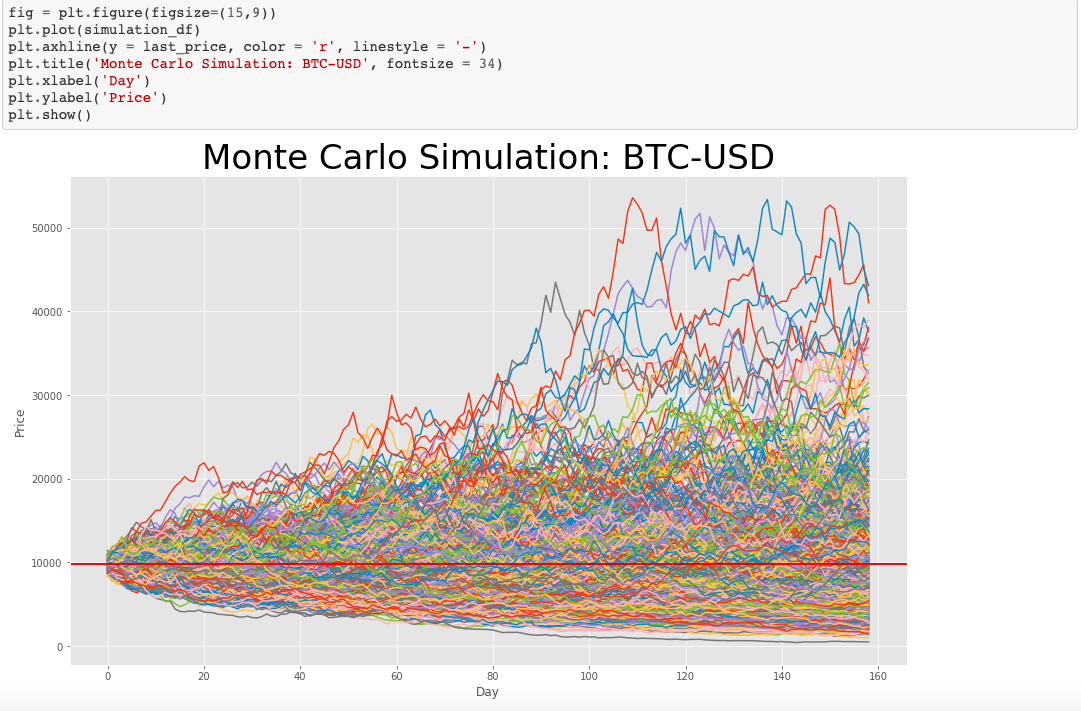
Messy graph representing Monte Carlo simulation, source: Bitcoin Monte Carlo Simulation

Conclusion

Monte Carlo simulations represent a powerful analytical tool in the arsenal of token engineers. By leveraging the principles of statistics, these simulations provide deep insights into the complex dynamics of token-based systems. This method allows for a nuanced understanding of potential future scenarios and helps with making informed decisions.

We encourage all stakeholders in the blockchain and cryptocurrency space to consider implementing Monte Carlo simulations. The insights gained from such analytical techniques can lead to more effective and resilient economic models, paving the way for the sustainable growth and success of digital currencies.

If you're looking to create a robust tokenomics model and go through institutional-grade testing please reach out to contact@nextrope.com. Our team is ready to help you with the token engineering process and ensure your project’s resilience in the long term.

FAQ

What is a Monte Carlo simulation in tokenomics context?

  • It's a mathematical method that uses random sampling to predict uncertain outcomes.

What are the benefits of using Monte Carlo simulations in tokenomics?

  • These simulations help foresee potential market scenarios, aiding in strategic planning and risk management for token launches.

Why are Monte Carlo simulations unique in cryptocurrency analysis?

  • They provide probabilistic outcomes rather than fixed predictions, effectively simulating real-world market variability and risk.

Tagi

Most viewed

Never miss a story

Stay updated about Nextrope news as it happens.

You are subscribed

Applying Game Theory in Token Design

Kajetan Olas

16 Apr 2024
Applying Game Theory in Token Design

Blockchain technology allows for aligning incentives among network participants by rewarding desired behaviors with tokens.
But there is more to it than simply fostering cooperation. Game theory allows for designing incentive-machines that can't be turned-off and resemble artificial life.

Emergent Optimization

Game theory provides a robust framework for analyzing strategic interactions with mathematical models, which is particularly useful in blockchain environments where multiple stakeholders interact within a set of predefined rules. By applying this framework to token systems, developers can design systems that influence the emergent behaviors of network participants. This ensures the stability and effectiveness of the ecosystem.

Bonding Curves

Bonding curves are tool used in token design to manage the relationship between price and token supply predictably. Essentially, a bonding curve is a mathematical curve that defines the price of a token based on its supply. The more tokens that are bought, the higher the price climbs, and vice versa. This model incentivizes early adoption and can help stabilize a token’s economy over time.

For example, a bonding curve could be designed to slow down price increases after certain milestones are reached, thus preventing speculative bubbles and encouraging steadier, more organic growth.

The Case of Bitcoin

Bitcoin’s design incorporates game theory, most notably through its consensus mechanism of proof-of-work (PoW). Its reward function optimizes for security (hashrate) by optimizing for maximum electricity usage. Therefore, optimizing for its legitimate goal of being secure also inadvertently optimizes for corrupting natural environment. Another emergent outcome of PoW is the creation of mining pools, that increase centralization.

The Paperclip Maximizer and the dangers of blockchain economy

What’s the connection between AI from the story and decentralized economies? Blockchain-based incentive systems also can’t be turned off. This means that if we design an incentive system that optimizes towards a wrong objective, we might be unable to change it. Bitcoin critics argue that the PoW consensus mechanism optimizes toward destroying planet Earth.

Layer 2 Solutions

Layer 2 solutions are built on the understanding that the security provided by this core kernel of certainty can be used as an anchor. This anchor then supports additional economic mechanisms that operate off the blockchain, extending the utility of public blockchains like Ethereum. These mechanisms include state channels, sidechains, or plasma, each offering a way to conduct transactions off-chain while still being able to refer back to the anchored security of the main chain if necessary.

Conceptual Example of State Channels

State channels allow participants to perform numerous transactions off-chain, with the blockchain serving as a backstop in case of disputes or malfeasance.

Consider two players, Alice and Bob, who want to play a game of tic-tac-toe with stakes in Ethereum. The naive approach would be to interact directly with a smart contract for every move, which would be slow and costly. Instead, they can use a state channel for their game.

  1. Opening the Channel: They start by deploying a "Judge" smart contract on Ethereum, which holds the 1 ETH wager. The contract knows the rules of the game and the identities of the players.
  2. Playing the Game: Alice and Bob play the game off-chain by signing each move as transactions, which are exchanged directly between them but not broadcast to the blockchain. Each transaction includes a nonce to ensure moves are kept in order.
  3. Closing the Channel: When the game ends, the final state (i.e., the sequence of moves) is sent to the Judge contract, which pays out the wager to the winner after confirming both parties agree on the outcome.

A threat stronger than the execution

If Bob tries to cheat by submitting an old state where he was winning, Alice can challenge this during a dispute period by submitting a newer signed state. The Judge contract can verify the authenticity and order of these states due to the nonces, ensuring the integrity of the game. Thus, the mere threat of execution (submitting the state to the blockchain and having the fraud exposed) secures the off-chain interactions.

Game Theory in Practice

Understanding the application of game theory within blockchain and token ecosystems requires a structured approach to analyzing how stakeholders interact, defining possible actions they can take, and understanding the causal relationships within the system. This structured analysis helps in creating effective strategies that ensure the system operates as intended.

Stakeholder Analysis

Identifying Stakeholders

The first step in applying game theory effectively is identifying all relevant stakeholders within the ecosystem. This includes direct participants such as users, miners, and developers but also external entities like regulators, potential attackers, and partner organizations. Understanding who the stakeholders are and what their interests and capabilities are is crucial for predicting how they might interact within the system.

Stakeholders in blockchain development for systems engineering

Assessing Incentives and Capabilities

Each stakeholder has different motivations and resources at their disposal. For instance, miners are motivated by block rewards and transaction fees, while users seek fast, secure, and cheap transactions. Clearly defining these incentives helps in predicting how changes to the system’s rules and parameters might influence their behaviors.

Defining Action Space

Possible Actions

The action space encompasses all possible decisions or strategies stakeholders can employ in response to the ecosystem's dynamics. For example, a miner might choose to increase computational power, a user might decide to hold or sell tokens, and a developer might propose changes to the protocol.

Artonomus, Github

Constraints and Opportunities

Understanding the constraints (such as economic costs, technological limitations, and regulatory frameworks) and opportunities (such as new technological advancements or changes in market demand) within which these actions take place is vital. This helps in modeling potential strategies stakeholders might adopt.

Artonomus, Github

Causal Relationships Diagram

Mapping Interactions

Creating a diagram that represents the causal relationships between different actions and outcomes within the ecosystem can illuminate how complex interactions unfold. This diagram helps in identifying which variables influence others and how they do so, making it easier to predict the outcomes of certain actions.

Artonomus, Github

Analyzing Impact

By examining the causal relationships, developers and system designers can identify critical leverage points where small changes could have significant impacts. This analysis is crucial for enhancing system stability and ensuring its efficiency.

Feedback Loops

Understanding feedback loops within a blockchain ecosystem is critical as they can significantly amplify or mitigate the effects of changes within the system. These loops can reinforce or counteract trends, leading to rapid growth or decline.

Reinforcing Loops

Reinforcing loops are feedback mechanisms that amplify the effects of a trend or action. For example, increased adoption of a blockchain platform can lead to more developers creating applications on it, which in turn leads to further adoption. This positive feedback loop can drive rapid growth and success.

Death Spiral

Conversely, a death spiral is a type of reinforcing loop that leads to negative outcomes. An example might be the increasing cost of transaction fees leading to decreased usage of the blockchain, which reduces the incentive for miners to secure the network, further decreasing system performance and user adoption. Identifying potential death spirals early is crucial for maintaining the ecosystem's health.

The Death Spiral: How Terra's Algorithmic Stablecoin Came Crashing Down
the-death-spiral-how-terras-algorithmic-stablecoin-came-crashing-down/, Forbes

Conclusion

The fundamental advantage of token-based systems is being able to reward desired behavior. To capitalize on that possibility, token engineers put careful attention into optimization and designing incentives for long-term growth.

FAQ

  1. What does game theory contribute to blockchain token design?
    • Game theory optimizes blockchain ecosystems by structuring incentives that reward desired behavior.
  2. How do bonding curves apply game theory to improve token economics?
    • Bonding curves set token pricing that adjusts with supply changes, strategically incentivizing early purchases and penalizing speculation.
  3. What benefits do Layer 2 solutions provide in the context of game theory?
    • Layer 2 solutions leverage game theory, by creating systems where the threat of reporting fraudulent behavior ensures honest participation.

Tagi

Token Engineering Process

Kajetan Olas

13 Apr 2024
Token Engineering Process

Token Engineering is an emerging field that addresses the systematic design and engineering of blockchain-based tokens. It applies rigorous mathematical methods from the Complex Systems Engineering discipline to tokenomics design.

In this article, we will walk through the Token Engineering Process and break it down into three key stages. Discovery Phase, Design Phase, and Deployment Phase.

Table of Contents

Discovery Phase of Token Engineering Process

The first stage of the token engineering process is the Discovery Phase. It focuses on constructing high-level business plans, defining objectives, and identifying problems to be solved. That phase is also the time when token engineers first define key stakeholders in the project.

Defining the Problem

This may seem counterintuitive. Why would we start with the problem when designing tokenomics? Shouldn’t we start with more down-to-earth matters like token supply? The answer is No. Tokens are a medium for creating and exchanging value within a project’s ecosystem. Since crypto projects draw their value from solving problems that can’t be solved through TradFi mechanisms, their tokenomics should reflect that. 

The industry standard, developed by McKinsey & Co. and adapted to token engineering purposes by Outlier Ventures, is structuring the problem through a logic tree, following MECE.
MECE stands for Mutually Exclusive, Collectively Exhaustive. Mutually Exclusive means that problems in the tree should not overlap. Collectively Exhaustive means that the tree should cover all issues.

In practice, the “Problem” should be replaced by a whole problem statement worksheet. The same will hold for some of the boxes.
A commonly used tool for designing these kinds of diagrams is the Miro whiteboard.

Identifying Stakeholders and Value Flows in Token Engineering

This part is about identifying all relevant actors in the ecosystem and how value flows between them. To illustrate what we mean let’s consider an example of NFT marketplace. In its case, relevant actors might be sellers, buyers, NFT creators, and a marketplace owner. Possible value flow when conducting a transaction might be: buyer gets rid of his tokens, seller gets some of them, marketplace owner gets some of them as fees, and NFT creators get some of them as royalties.

Incentive Mechanisms Canvas

The last part of what we consider to be in the Discovery Phase is filling the Incentive Mechanisms Canvas. After successfully identifying value flows in the previous stage, token engineers search for frictions to desired behaviors and point out the undesired behaviors. For example, friction to activity on an NFT marketplace might be respecting royalty fees by marketplace owners since it reduces value flowing to the seller.

source: https://www.canva.com/design/DAFDTNKsIJs/8Ky9EoJJI7p98qKLIu2XNw/view#7

Design Phase of Token Engineering Process

The second stage of the Token Engineering Process is the Design Phase in which you make use of high-level descriptions from the previous step to come up with a specific design of the project. This will include everything that can be usually found in crypto whitepapers (e.g. governance mechanisms, incentive mechanisms, token supply, etc). After finishing the design, token engineers should represent the whole value flow and transactional logic on detailed visual diagrams. These diagrams will be a basis for creating mathematical models in the Deployment Phase. 

Token Engineering Artonomous Design Diagram
Artonomous design diagram, source: Artonomous GitHub

Objective Function

Every crypto project has some objective. The objective can consist of many goals, such as decentralization or token price. The objective function is a mathematical function assigning weights to different factors that influence the main objective in the order of their importance. This function will be a reference for machine learning algorithms in the next steps. They will try to find quantitative parameters (e.g. network fees) that maximize the output of this function.
Modified Metcalfe’s Law can serve as an inspiration during that step. It’s a framework for valuing crypto projects, but we believe that after adjustments it can also be used in this context.

Deployment Phase of Token Engineering Process

The Deployment Phase is final, but also the most demanding step in the process. It involves the implementation of machine learning algorithms that test our assumptions and optimize quantitative parameters. Token Engineering draws from Nassim Taleb’s concept of Antifragility and extensively uses feedback loops to make a system that gains from arising shocks.

Agent-based Modelling 

In agent-based modeling, we describe a set of behaviors and goals displayed by each agent participating in the system (this is why previous steps focused so much on describing stakeholders). Each agent is controlled by an autonomous AI and continuously optimizes his strategy. He learns from his experience and can mimic the behavior of other agents if he finds it effective (Reinforced Learning). This approach allows for mimicking real users, who adapt their strategies with time. An example adaptive agent would be a cryptocurrency trader, who changes his trading strategy in response to experiencing a loss of money.

Monte Carlo Simulations

Token Engineers use the Monte Carlo method to simulate the consequences of various possible interactions while taking into account the probability of their occurrence. By running a large number of simulations it’s possible to stress-test the project in multiple scenarios and identify emergent risks.

Testnet Deployment

If possible, it's highly beneficial for projects to extend the testing phase even further by letting real users use the network. Idea is the same as in agent-based testing - continuous optimization based on provided metrics. Furthermore, in case the project considers airdropping its tokens, giving them to early users is a great strategy. Even though part of the activity will be disingenuine and airdrop-oriented, such strategy still works better than most.

Time Duration

Token engineering process may take from as little as 2 weeks to as much as 5 months. It depends on the project category (Layer 1 protocol will require more time, than a simple DApp), and security requirements. For example, a bank issuing its digital token will have a very low risk tolerance.

Required Skills for Token Engineering

Token engineering is a multidisciplinary field and requires a great amount of specialized knowledge. Key knowledge areas are:

  • Systems Engineering
  • Machine Learning
  • Market Research
  • Capital Markets
  • Current trends in Web3
  • Blockchain Engineering
  • Statistics

Summary

The token engineering process consists of 3 steps: Discovery Phase, Design Phase, and Deployment Phase. It’s utilized mostly by established blockchain projects, and financial institutions like the International Monetary Fund. Even though it’s a very resource-consuming process, we believe it’s worth it. Projects that went through scrupulous design and testing before launch are much more likely to receive VC funding and be in the 10% of crypto projects that survive the bear market. Going through that process also has a symbolic meaning - it shows that the project is long-term oriented.

If you're looking to create a robust tokenomics model and go through institutional-grade testing please reach out to contact@nextrope.com. Our team is ready to help you with the token engineering process and ensure your project’s resilience in the long term.

FAQ

What does token engineering process look like?

  • Token engineering process is conducted in a 3-step methodical fashion. This includes Discovery Phase, Design Phase, and Deployment Phase. Each of these stages should be tailored to the specific needs of a project.

Is token engineering meant only for big projects?

  • We recommend that even small projects go through a simplified design and optimization process. This increases community's trust and makes sure that the tokenomics doesn't have any obvious flaws.

How long does the token engineering process take?

  • It depends on the project and may range from 2 weeks to 5 months.

Tagi